I. Logique booléenne :
I.1 Définition :
Beaucoup de systèmes automatisés fonctionnent en utilisant des organes et des fonctions
binaires. Ces organes et fonctions binaires ne peuvent être que dans deux états possibles.
Par exemple, un détecteur de niveau peut être immergé ou submergé. Un voyant peut être
allumé ou éteint.
Par convention, on représente par la valeur logique « 0 » l’un de ces états et par la valeur
logique « 1 » l’autre état. La valeur logique « 0 » correspond à un organe binaire (ou une
fonction binaire) dans un état dit « non-activé », « non-actionné » ou « inactif »
(exemple : un voyant inactif est éteint). La valeur logique « 1 » correspond à un organe
binaire (ou une fonction binaire) dans un état dit « activé », « actionné » ou « actif »
(exemple : un voyant actif est allumé).
La mathématique des fonctions binaires est appelée l’algèbre booléenne, elle définit
trois opérateurs de base ainsi qu’une foule de règles et de postulats. Ainsi, toutes les
fonctions binaires (dites aussi logiques) sont des relations entre des entrées et des sorties
logiques composées d’opérateurs de base et sur lesquelles on peut appliquer diverses
règles d’algèbre de Boole.
I.2 Les lois de l’algèbre de Boole
I.3 Les Théorèmes de l’algèbre de Boole :
I.4 Postulats de l’algèbre de Boole :
I.5 Simplification algébrique des équations booléennes : La simplification d’une équation revient à appliquer les règles :
- Des opérations booléennes.
- Des relations fondamentales.
- Du théorème de MORGAN.
Et à utiliser, éventuellement, comme moyens de simplification le tableau ou diagramme de
Karnaugh.
Exemple :
simplifier : z = (a + b) ( b + c ) ( a + c )
z = (a b +a c + b b +b c ) ( a + c)
Or, b b = 0
z = (a b +a c + b c ) ( a + c) développons, on aura :
z = a b a +a b c + a c a + a c c + b c a + b c c
Or, a a = 0 a b a = 0 a a c = 0 et c c = c
z = a b c + a b c + a c + b c
z = c [ a ( b + 1) + b ( a +1) ]
Or, a + 1 = b +1=1
z = (a + b ) c
II. Les systèmes de numération :
II.1 Base d’un système de numération:
La base d’un système de numération est le nombre de chiffres différents qu’utilise ce
système de numération. En électronique numérique, les systèmes les plus couramment
utilisés sont : le système binaire, le système octal, le système décimal et le système
hexadécimal.
Se rappeler que : a0 = 1.
a) Système décimal :
C’est le système de numération décimal que nous utilisons tous les jours. C’est le
système de base 10 qui utilise donc 10 symboles différents : 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9.
Un nombre N (entier positif) exprimé dans le système de numération décimal est défini par
la relation ci-dessous :
N = an x 10n + an-1 x 10n-1 .............. + a0 x 100
(où an est un chiffre de rang n)
Exemple : N = (1975)10
N = 1 x 103 + 9 x 102 + 7 x 101 + 5 x 100
Les puissances de 10 sont appelées les poids ou les valeurs de position. Le poids est
égal à la base élevée à la puissance de son rang.
b) Système binaire Le système binaire est le système de base 2, c’est à dire qui utilise deux symboles
différents : le 0 et le 1. Chacun d’eux est appelé bit ou élément binaire.
Dans ce système, le poids est une puissance de 2.
Exemple : • Puissance de 2 : Triplet : nombre binaire formé de 3 éléments binaires.
Quartet : nombre binaire formé de 4 éléments binaires.
Octet (byte) : nombre binaire formé de 8 éléments binaires.
Mot (word) : nombre binaire formé de 16 éléments binaires.
L.S.B. : bit le moins significatif ou bit de poids faible (élément le plus à droite d’un nombre
binaire).
M.S.B. : bit le plus significatif ou bit de poids fort (élément binaire le plus à gauche d’un
nombre binaire).
c) Système octal
Le système de numération octal est de base 8, ainsi il utilise 8 symboles différents : 0, 1,
2, 3, 4, 5, 6 et 7.
Dans ce système, le poids est une puissance de 8.
Exemple : La succession des nombres par ordre croissant est le suivant :
- 1 chiffre : 0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2.......etc.
- 2 chiffres : 10, 11, 12, 13, 14, 15, 16, 17, 20, 21......, 27, 30, 31....etc.
• Puissance de 8 :
d) Système hexadécimal Le système hexadécimal est de base 16 et utilise 16 symboles différents : les dix premiers
chiffres décimaux : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 et les 6 premières lettres de l’alphabet : A, B,
C, D, E, F.
La succession des nombres hexadécimaux par ordre croissant est la suivante :
- 1 chiffre : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 0, 1, 2, 3.....etc.
- 2 chiffres : 00, 01, 02 ....., 09, 0A, 0B,....., 0F, 10, 11, 12,....., 19, 1A, 1B.....etc.
Les lettres de A à F correspondent respectivement aux nombres décimaux 10 à 15.
Dans ce système, le poids est une puissance de 16.
Exemple :
• Puissance de 16 :
II.2 Changement de base :
a) Conversion des bases 2, 8 ou 16 en base 10
Pour convertir un nombre de la base 2, 8 ou 16 en nombre de base 10, il suffit de décomposer le nombre en ses quantités et d’en faire la somme.
Exemple :
Tableau de correspondance entre nombre de différentes bases
b) Conversion d’un nombre décimal en un nombre d’un système d’une autre base
Cette conversion se fait en deux parties :
1- La partie entière.
2- La partie fractionnaire.
Problème : Un nombre N étant donné en base 10, cherchons à l’écrire dans un système de base b.
- On traite d’abord la partie entière :
Pour la partie entière nous la divisons par la base b et nous conservons le reste. Le quotient obtenu est divisé par b et nous conservons le reste. Il faut répéter l’opération sur chaque quotient obtenu. Les restes successifs sont écrits, en commençant par le dernier, de la gauche vers la droite pour former l’expression de N dans le système de base b.
- On traite après la partie fractionnaire :
Exemple 1 : Conversion du nombre (3786, 4) 10 en base 2 :
- On traite d’abord la partie entière :3786
Le nombre binaire ainsi obtenu est :

- On traite après la partie fractionnaire :
D’où (0, 4)10 = (0, 01100)2
Résultat : (3786, 4)10 = (111011001010, 01100)2
Exemple 2 : (459, 3)10 le convertir en base 8.
- Partie entière :
(459)10 = (713)8
- Partie fractionnaire :
(0, 3)
10 = (0, 2314)
8
Résultat : ( 459, 3)10 = (713, 2314)8
c) Autres conversions
• Conversion d’un nombre octal en un nombre binaire :
Chaque symbole du nombre écrit dans le système octal est remplacé par son équivalent écrit dans le système binaire à trois bits (voir tableau de correspondance).
Exemple : N = (257)8 = (010 101 111)2
2 5 7
• Conversion d'un nombre binaire en un nombre octal :
C’est l’opération inverse de la précédente. Il faut regrouper les 1 et 0 du nombre trois par trois en commençant par la droite, puis chaque groupe est remplacé par le chiffre octal correspondant.
Exemple : N = (11001101111)2 = 11 001 101 111
3 1 5 7
N = (3157)8
• Conversion d’un nombre hexadécimal en un nombre binaire :
Chaque symbole du nombre hexadécimal est remplacé par son équivalent écrit sur quatre bits dans le système binaire.
Exemple : N = (B F 8)
16 N = (1011 1111 1000)2
B F 8
• Conversion d'un nombre binaire en un nombre hexadécimal :
C’est l’inverse de la précédente. Il faut donc regrouper les 1 et 0 du nombre par quartet en commençant par la droite, puis chaque groupe est remplacé par le symbole hexadécimal correspondant.
Exemple : N = (100001101111)2
N = 1000 0110 1111
8 6 F
N = (86F)16
II.3 Opérations arithmétiques avec la base binaire:
a) Addition Binaire :
Les règles de base sont :
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 reporte 1
Exemple : 1 1 1 Reports
1101 0
+
1011 1
11000 1
b) Soustraction Binaire :
Les règles de base sont
0 - 0 = 0
0 - 1 = 1 Emprunte 1
1 - 0 = 1
1 - 1 = 0
Exemple : 0 Emprunt
11011 1
-
110 1
10101 0
c) Multiplication Binaire :
Les règles de base sont :
0 * 0 = 0
0 * 1 = 0
1 * 0 = 0
1 * 1 = 1
Exemple :
101
*
110
11110
d) Division Binaire :
Les règles de base sont :
0 / 0 = Indéterminé
0 / 1 = 0
1 / 0 = Impossible
1 / 1 = 1
Exemple :
1010 / 10
-10 101
001
-00
10
-10
00
II.4 Les codes :
a) Code binaire :
(Binary coded décimal) en français ( Décimal codé Binaire)
Exemple : (115) 10
(American standard code for information interchange)
Ou code américain pour l'échange d'information : c'est un code alphanumérique qui
permet de représenter des chiffres, des lettres ainsi que divers caractères spéciaux. Il
traduit ces caractères en langage machine.
Colonne C: caractère ASCII ou fonction de contrôle particulière.
Colonne D: décimal.
Colonne O: octal.
Colonne H: hexadécimal.
d) Code Gray :
(Code binaire réfléchi, ne peut être utilisé pour les opérations arithmétiques).
C'est une autre forme de la base binaire.
Un seul bit à la fois change d'état lorsqu'on passe d'un nombre au suivant.
III. Les fonctions logiques de base
III.1 Les trois fonctions logiques de base
Les fonctions logiques reposent sur trois opérateurs de base. Ce sont les fonctions logiques : « NON » (en anglais « NOT »), « ET » (en anglais « AND ») et « OU » (en anglais « OR »). Nous les présentons avec leurs équations et leurs tables de vérité.
a) La fonction logique « NON » :
Soit une variable booléenne nommée A. La fonction logique NON (A), appelé complément de A, sera notée A (lire A barre).
Le résultat de NON (A) sera également une variable booléenne.
La table ci-contre est la table de vérité de cette fonction.
Au niveau algébrique, l’équation correspondant à cette table de vérité est: F = A
b) La fonction logique « ET » :
Soit deux variables booléennes nommées A et B. Le résultat de la fonction logique A ET B sera également une variable booléenne. Le tableau de droite montre la table de vérité de cette fonction. la fonction logique
ET n’active la sortie que lorsque toutes les entrées sont actives.
Au niveau algébrique, l’équation correspondant à cette table de vérité est F = A•B . Le symbole du ET est semblable à celui du produit.
c) La fonction logique « OU » :
Soit deux variables booléennes nommées A et B. Le résultat de la fonction logique A OU B sera également une variable booléenne. La table de vérité de cette fonction est montrée à droite. La fonction logique OU donne une valeur de sortie égale à 1 dès qu’une des entrées est à 1.
Au niveau algébrique, l’équation correspondant à cette table de vérité est F = A+B . Le symbole du OU est semblable à celui de la somme.
III.2 Les autres fonctions logiques :
En plus des opérateurs de base, il existe d'autres opérateurs de deux variables et nous présentons ici les plus importants.
a) Opérateur « OUI » ou opérateur égalité
La sortie est à l’état 1 si, et seulement si, l’entrée est à l’état 1.
b) La fonction logique « NON-ET » :
Soit deux variables booléennes nommées A et B. Le résultat de la fonction logique NON( A ET B) sera également une variable booléenne. La figure de droite montre la table de vérité de cette fonction. La sortie de la fonction logique NON-ET (en anglais NAND) a un comportement inverse à celle de la fonction logique ET.
Au niveau algébrique, l’équation correspondant à cette table de vérité est F = A•B . L’ajout de la barre au-dessus de la fonction traduit ainsi l’inversion du résultat du ET.
c) La fonction logique « NON-OU »
Soit deux variables booléennes nommées A et B. Le résultat de la fonction logique NON (A OU B) sera également une variable booléenne. La table ci-contre montre la table de vérité de cette fonction. La sortie de la fonction logique NON-OU (en anglais NOR) a un comportement inverse à celle de la fonction logique OU.
Au niveau algébrique, l’équation correspondant à cette table de vérité est F = A+B . L’ajout de la barre au-dessus de la fonction traduit ainsi l’inversion du résultat du OU.
Remarque :
Ces deux fonctions (NON-ET et NON-OU) sont très utilisées en électronique, car elles représentent des éléments de connections universels. Toute fonction logique peut en effet être écrite exclusivement à partir de l’une ou l’autre de ces fonctions. Un des avantages de ces éléments de connexion universel est de permettre l’implantation de n’importe quelle fonction logique à l’aide d’un seul type de circuit électronique. Il y a donc standardisation sur un seul type de circuit électronique. Ainsi, il est possible d’en acheter une grande quantité pour bénéficier d’un prix de vente avantageux. On ne stocke qu’un seul type de circuit en prévision d’éventuelles pannes .
d) La fonction logique « OU-EXCLUSIF »
Soit deux variables booléennes nommées A et B. Le résultat de la fonction logique A OUEXCLUSIF B sera également une variable booléenne. La table de vérité de droite montre le comportement de cette fonction.
la sortie de la fonction logique OUEXCLUSIF (en anglais EXOR) ne donne un niveau logique 1 que si, et seulement si, une seule entrée est à l’état 1.
Au niveau algébrique, l’équation correspondant à cette table de vérité est F = A⊕B .
Cette expression peut aussi être écrite sous une autre forme :
e) La fonction logique « NON-OU-EXCLUSIF »
Soit deux variables booléennes nommées A et B. Le résultat de la fonction logique NON (A OUEXCLUSIF B) sera également une variable booléenne. La figure de droite montre la table de vérité de cette fonction. La sortie de la fonction logique NON-OUEXCLUSIF est l’inverse de celle obtenue avec la fonction logique OU-EXCLUSIF.
Au niveau algébrique, l’équation correspondant à cette table de vérité est
III.3 Les fonctions logiques matérialisées avec des interrupteurs:
Comme il était mentionné précédemment un interrupteur est un organe binaire pouvant être actionné (lorsque l’opérateur appui dessus), ou non-actionné (lorsque l’opérateur n’y touche pas). Selon le type d’interrupteur, il peut être actionné par un opérateur (bouton de commande), par un mécanisme (interrupteur de fin de course), par la détection de la présence d’une grandeur physique (détecteur de niveau, de température, ...).
Dans sa position de repos, un interrupteur peut laisser passer ou non le courant électrique. Si l’interrupteur doit être actionné pour qu’il laisse passer le courant, nous avons un interrupteur dit « normalement ouvert ». Par contre, si en actionnant l’interrupteur le courant est coupé (ou ne passe plus), nous avons un interrupteur dit « normalement fermé »
Une ampoule (ou un voyant) est un organe binaire qui peut être actionné (lorsque le courant passe et que l’ampoule est allumée), ou non-actionné (lorsque le courant ne passe plus et que l’ampoule est éteinte).
Dans la suite nous verrons comment, en utilisant les interrupteurs comme entrées logiques et une ampoule comme sortie obtenir des fonctions logiques.
a) Fonction logique « OUI »
La figure ci-dessous montre la fonction logique OUI. Cette fonction utilise simplement un interrupteur normalement ouvert. Le voyant s’allumera si l’interrupteur est actionné.
La fonction logique de ce montage est : L = a
b) Fonction logique « NON »
La figure ci-dessous montre la fonction logique NON. Pour obtenir cette fonction, il suffit de brancher un interrupteur normalement fermé. Le voyant s’allume tant que l’interrupteur n’est pas actionné.
La fonction logique de ce montage est :
c) Fonction logique « ET »
La figure ci-dessous montre la fonction logique ET. Pour obtenir cette fonction, il suffit de branche deux interrupteurs normalement ouverts en série. Pour que le courant puisse traverser le voyant et l’allume, il faut actionner simultanément les deux interrupteurs.
La fonction logique de ce montage est : L = a•b
d) Fonction logique « OU »
La figure ci-dessous montre la fonction logique OU. Pour obtenir cette fonction, il suffit de brancher deux interrupteurs normalement ouverts en parallèle. Le voyant s’allume dès que l’un des interrupteurs est actionné.
La fonction logique de ce montage est : L = a + b
e) Fonction logique « NON-ET »
La figure ci-dessous montre la fonction logique NON-ET. Pour obtenir cette fonction, il suffit de brancher deux interrupteurs normalement fermés en parallèle. Le voyant s’éteint seulement si les deux interrupteurs sont actionnés simultanément.
La fonction logique de ce montage est :
f) Fonction logique « NON-OU »
La figure ci-dessous montre la fonction logique NON-OUT. Pour obtenir cette fonction, il suffit de brancher deux interrupteurs normalement fermés en série. Le voyant s’éteint dès qu’un des interrupteurs est actionné.
La fonction logique de ce montage est :
g) Fonction logique « OU-EXCLUSIF »
La figure ci-dessous montre la fonction logique OU-EXCLUSIF. Pour obtenir cette fonction, il suffit de brancher, tel que montré, deux interrupteurs ayant deux contacts chacun, l’un normalement ouvert, l’autre normalement fermé. Le voyant s’allume si et seulement si un seul interrupteur est actionné.
La fonction logique de ce montage est :
ou encore :
h) Fonction logique « NON-OU-EXCLUSIF »
La figure ci-dessous montre la fonction logique NON-OU-EXCLUSIF. Pour obtenir cette fonction, il suffit de brancher, tel que montré, deux interrupteurs ayant deux contacts chacun, l’un normalement ouvert, l’autre normalement fermé. Le voyant s’éteint si et seulement si un seul interrupteur est actionné.
La fonction logique de ce montage est :
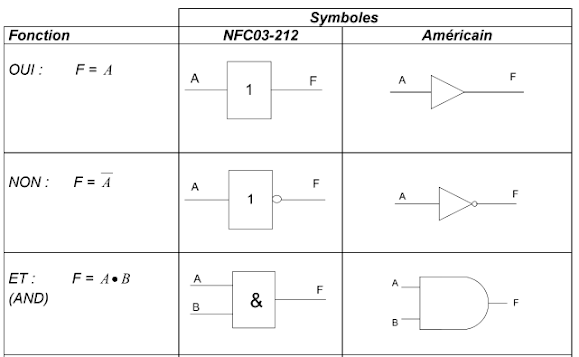
III.4 Symbolisation
IV. Table de vérité
IV.1 Tableau des combinaisons
De nombreux circuits logiques possèdent plusieurs entrées mais seulement une sortie.
Une table de vérité nous fait connaître la réaction d’un circuit logique (sa valeur de sortie)
aux diverses combinaisons de niveaux logiques appliqués aux entrées.
Pour une table de N entrés il y a 2N lignes.
On peut construire un tableau de ces combinaisons comportant autant de colonnes que de
variables d’entrées et autant de lignes que de combinaisons.
Pour le remplir, il suffit d’écrire pour chaque ligne l’équivalent binaire des nombres
décimaux à compter de 0 à 2 n – 1.
Exemple :
a) 2 variables A et B on a 22 = 4 combinaisons à compter de 0 à 3.
b) 3 variables A, B et C on a 23 = 8 combinaisons à compter de 0 à 7.







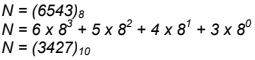








































Aucun commentaire:
Enregistrer un commentaire